Draw Equilateral Triangle in a Circle

Use only your compass and directly edge when drawing a structure. No free-hand drawing!

We will be doing THREE constructions of an equilateral triangle. The first volition exist to construct an equilateral triangle given the length of i side, and the other ii will be to construct an equilateral triangle inscribed in a circle.

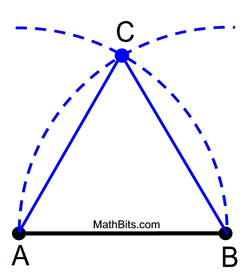
Given: the length of one side of the triangle Construct: an equilateral triangle

STEPS:
1. Place your compass point on A and measure the distance to point B. Swing an arc of this size above (or below) the segment.
2. Without changing the span on the compass, identify the compass bespeak on B and swing the same arc, intersecting with the first arc.
3. Label the point of intersection as the third vertex of the equilateral triangle.

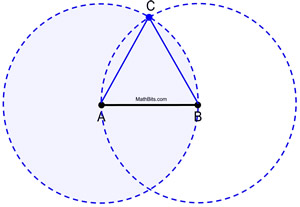
See the total circles at work.

Proof of Structure: Circle A is congruent to circle B, since they were each formed using the same radius length, AB. Since AB and Ac are lengths of radii of circumvolve A, they are equal to i another. Similarly, AB and BC are radii of circumvolve B, and are equal to one another. Therefore, AB = AC = BC past substitution (or transitive property). Since congruent segments have equal lengths, and ΔABC is equilateral (having three congruent sides).

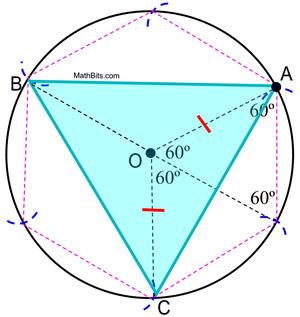
Given: a piece of paper Construct: an equilateral triangle inscribed in a circle.

This is a modification of the construction of a regular hexagon inscribed in a circle.

STEPS:
one. Identify your compass point on the newspaper and draw a circle. (Go on this compass span!)
ii. Place a dot, labeled A, anywhere on the circumference of the circle to act equally a starting point.
3. Without irresolute the span on the compass, place the compass point on A and swing a small arc crossing the circumference of the circumvolve.
4. Without changing the span on the compass, movement the compass point to the intersection of the previous arc and the circumference and brand some other small arc on the circumference of the circle.
5. Keep repeating this process of "stepping" around the circle until you return to point A.
6. Starting at A, connect every other arc on the circle to course the equilateral triangle.

Proof of Construction: The proof of the inscribed regular hexagon shows that the central angles of a regular hexagon contain 60º. The central angles of the triangle inscribed in this circle comprise 120º. Since ΔAOC is isosceles (OA and OC are radii lengths), one thousand∠OCA = 1000∠OAC = ½ (180 - 120) = 30º. ΔAOC ΔCOB ΔBOA by SAS. By CPCTC, ∠OCB ∠OCA and grand∠OCB = 30º by substitution and thousand∠BCA = 60º. In like way, we take m∠ACB = m∠CBA = m∠BAC = 60º and equilateral ΔABC.

Given: a slice of paper Construct: an equilateral triangle inscribed in a circle.

This method uses noesis of the special correct triangle 30º - 60º - 90º.

STEPS:
1. Identify your compass signal on the newspaper and describe a circle, O. (Keep this compass span!)
2. Using a straightedge, depict a diameter of the circle, labeling the endpoints P and B.
iii. Without irresolute the span on the compass, place the compass bespeak on P and draw a full circle.
four. Label the points of intersection of the two circle circumferences with A and C.
5. Draw segments from A to B, B to C and C to A, to form the equilateral triangle.

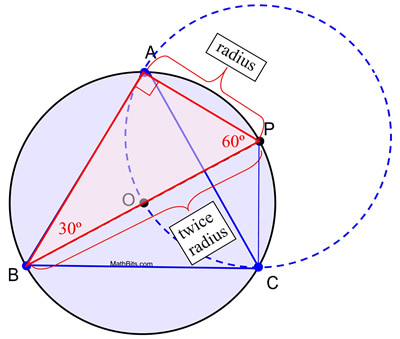
Proof of Structure: This construction uses the fact that an bending inscribed in a semicircle is a correct angle, and that in a 30º-60º-90º triangle, the length of the short leg is half of the length of the hypotenuse. In this construction, circle O and circumvolve P are congruent since they have the same radius length. AP is a radius length of circumvolve P and radii AP = OP. OP is likewise a radius length of circle O (forth with OB) and bore BP = BO + OP = 2 OP. By substitution, BP = 2 AP, creating the weather necessary for m∠ABP = 30º. Consequently, yard∠APB = 60º. A like statement tin can be used to found that for ΔPBC, one thousand∠ PBC = 30º and 1000∠BPC = 60º making ΔPBC ΔPBA by ASA (with shared side from B to P).
Now, since they are the corresponding sides of the two congruent triangles, making ΔABC isosceles. ∠BAC ∠BCA since the base of operations angles of an isosceles triangle are congruent.
m∠ABC = thousand∠ABP + m∠PBC = 30º + 30º = 60º past Angle Addition Postulate and substitution. grand∠BAC + m∠BCA + m∠ABC = 180º because the sum of the angle measures in a triangle is 180º. Since thou∠BAC + grand∠BAC + 60º = 180º by substitution, we know 2m∠BAC = 120º and m∠BAC = 60º. Consequently g∠BCA also equals 60º by substitution, making ΔABC equilateral.

Note: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
and is not considered "fair employ" for educators. Please read the "Terms of Utilize".

fernandesceshounce.blogspot.com

Source: https://mathbitsnotebook.com/Geometry/Constructions/CCconstructionEqui.html